Insertion Sort Algorithm Java.

Insertion Sort Algorithm: In this technique, given array is divided into two parts.

1. Sorted Sublist (array)

2. Unsorted Sublist (array)

Steps to follow During Insertion Sort Algorithm:

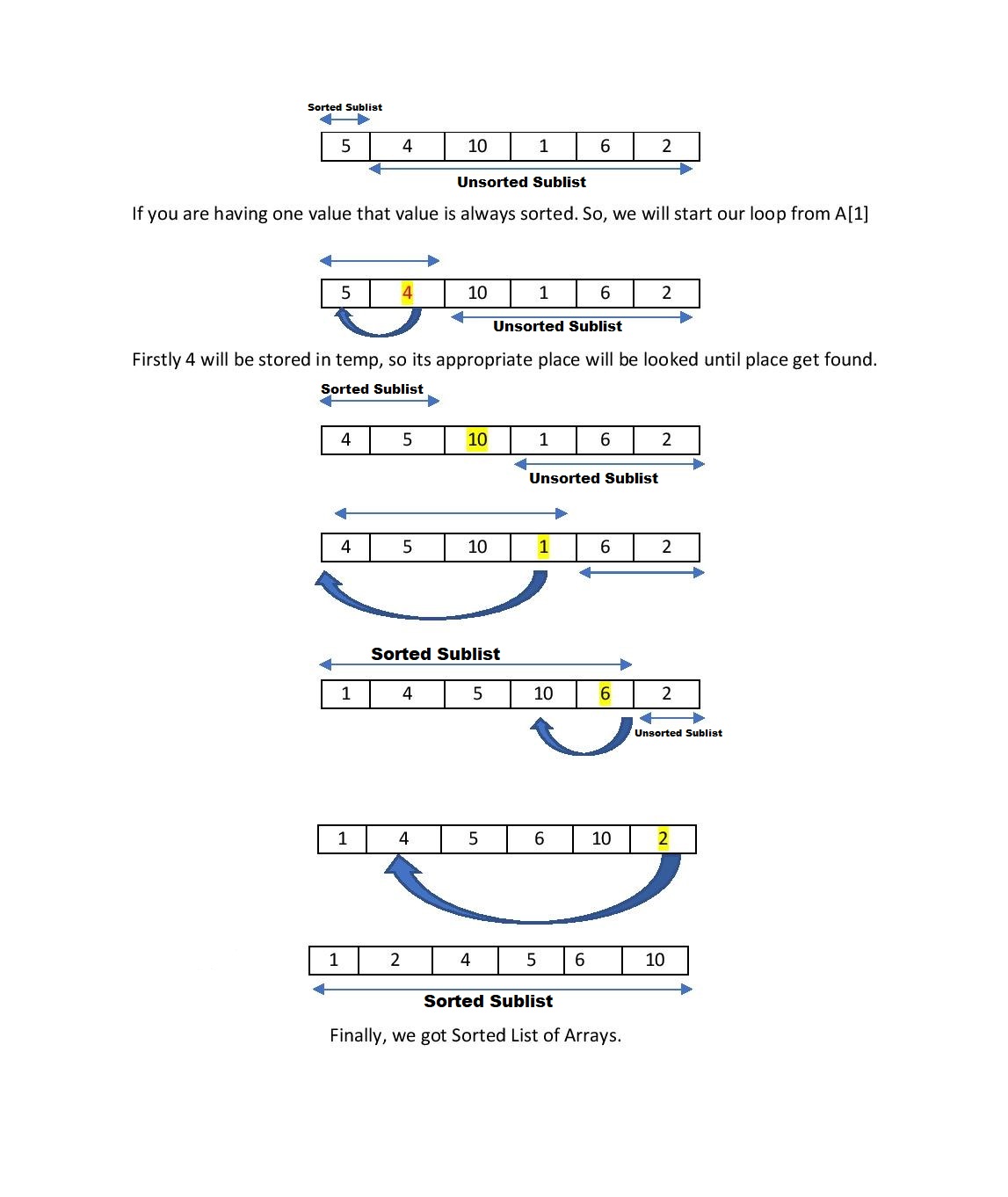
1. Firstly, we are going to pick one value from the unsorted sub list let us say we store that value in temp variable.
2. Then, we are going to find out the appropriate place for that value (say temp) in sorted sub list and push all bigger elements than temp one place ahead.
3. After finding, we will insert temp in Sorted Sub list in its correct place.

Shifting of elements will be done until j (second loop reaches 0).(Refer code)

Two loops will be required, one for increment of i and other for decrement of j (until j >= 0).
Remember: j is always intitialized one step behind than i.

Code:

• Java

public class InsertionSort {

    public static void main(String[] args) {

        int arr[] = { 100, 23, 1, 0, 45, 11, 78 };

        int n = arr.length;

        // calling insertionSort method which will make the array sorted

        insertionSort(arr, n);

        System.out.print("Sorted Arrays by using Insertion Sort Method: ");

        printSortedArray(arr, n); // for displaying the array

    }

    private static void insertionSort(int[] arr, int n) {

        for (int i = 1; i < n; i++) {

            int temp;

            temp = arr[i];

            int j; // j should be always one place behind i

            for (j = i - 1; j >= 0 && arr[j] > temp; j--) {

                arr[j + 1] = arr[j];

            }

            arr[j + 1] = temp;

        }

    }

    private static void printSortedArray(int[] arr, int n) {

        n = arr.length;

        for (int i = 0; i < n; i++)

            System.out.print(arr[i] + " ");

    }

}

Output:

Sorted Arrays by using Insertion Sort Method: 0 1 11 23 45 78 100

Complexity Analysis:

Time Complexity:
Worst Case: When array is given in descending order then time complexity isO(N²).
Best Case: When array is in ascending order or sorted, in that case time complexity will be O(N).
Space Complexity: O(1), we have not used any extra space.